Dans le cadre de leur projet mathématique de 3ème année,
des étudiants ont travaillé sur le concept de fractales. Cet article
présente quelques jolies figures qu’ils ont programmées
à l’aide du logiciel Maple.
Les fractales étudiées sont des fractales autosimilaires,
c’est-à-dire possédant la propriété suivante : la fractale
globale contient une infinité de copies d’elle-même à des
échelles allant jusqu’à l’infiniment petit.
Mathématiquement, il s’agit d’un objet limite obtenu en
itérant un processus. Pour déterminer le processus
permettant de construire une fractale donnée, il suffit de
déterminer les applications géométriques qui
transforment la fractale en des copies plus petites d’elle-même.
Le flocon de Von Koch, par exemple, peut être vu comme
l’union de 4 copies de lui-même 3 fois plus petites.
Déterminer les 4 transformations géométriques
(composées de rotations, translations, homothéties) correspondant
à ces réductions permet ensuite de construire le flocon.
Partant d’un segment, les étudiants ont itéré ces transformations.
On voit ci-dessous les premières étapes du processus et la
convergence vers la fractale finale.

Une fois les transformations programmées, on peut partir de n’importe
quelle figure géométrique, le processus convergera toujours vers la
même fractale. Ci-dessous, on obtient de nouveau le flocon de Von Koch
en partant d’un segment vertical.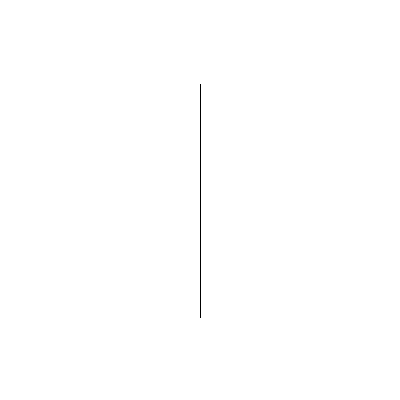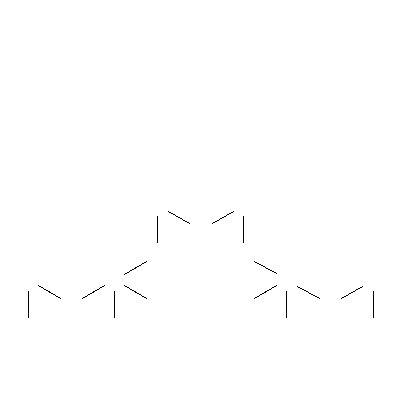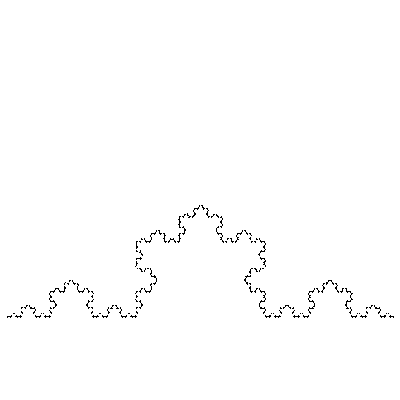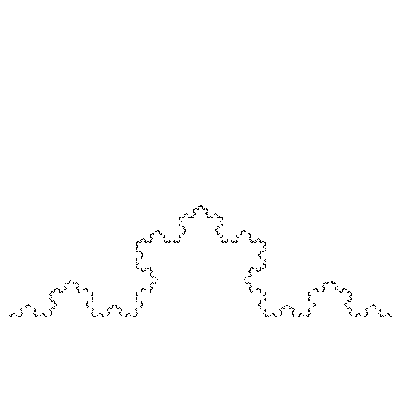
La fractale suivante est le triangle de Sierpinski. Pour l’obtenir, on peut le
voir comme une union de 3 copies de lui-même 2 fois plus petites.

Le même objet limite en démarrant le processus avec un carré.

Pour finir, voici d’autres fractales obtenues par les étudiants :
- Tapis de Sierpinski
- Fougère de Barnsley
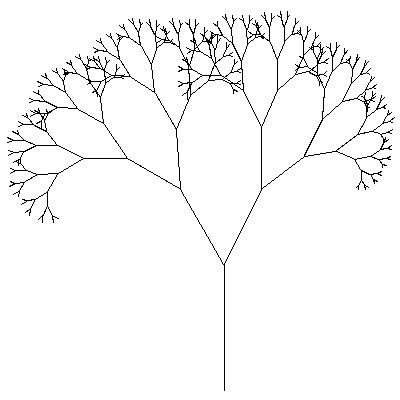
- Arbre de Pythagore
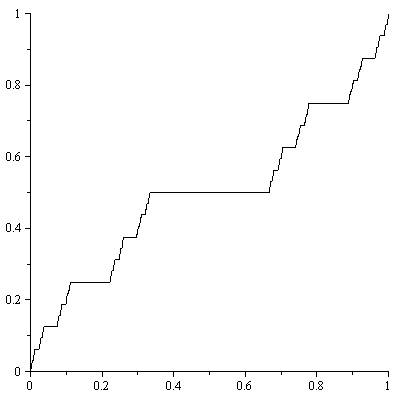
- Escalier du diable
- Courbe du dragon
- Arbre fractal
Les programmes pour obtenir ces images ont été réalisés par Antoine Bettenfeld, Quentin Hohmann, Martin Lefebvre, Cécile Robert, Tanguy Signardie et Mathilde Strubel, étudiantes et étudiants en troisième année de topographie, génie civil et génie mécanique.